Tic-Tac-Toe
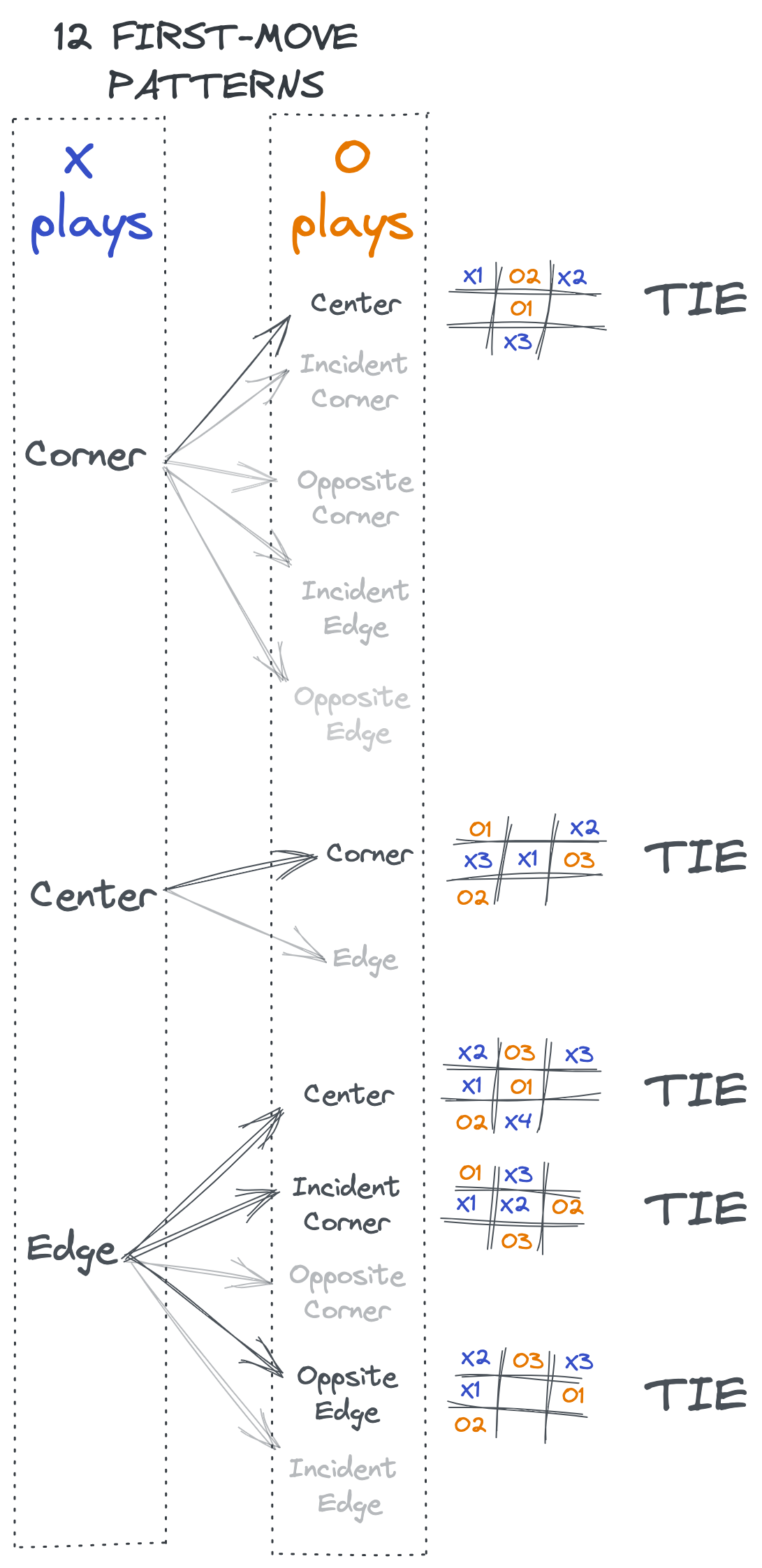
A tic-tac-toe game has 9 cells. “X” plays one of them as a first move and “O” plays one among the remaining 8 cells. In total there are 72 possible first-moves. But most of them are equivalent under rotations and reflections. There are 12 “different” first-moves.
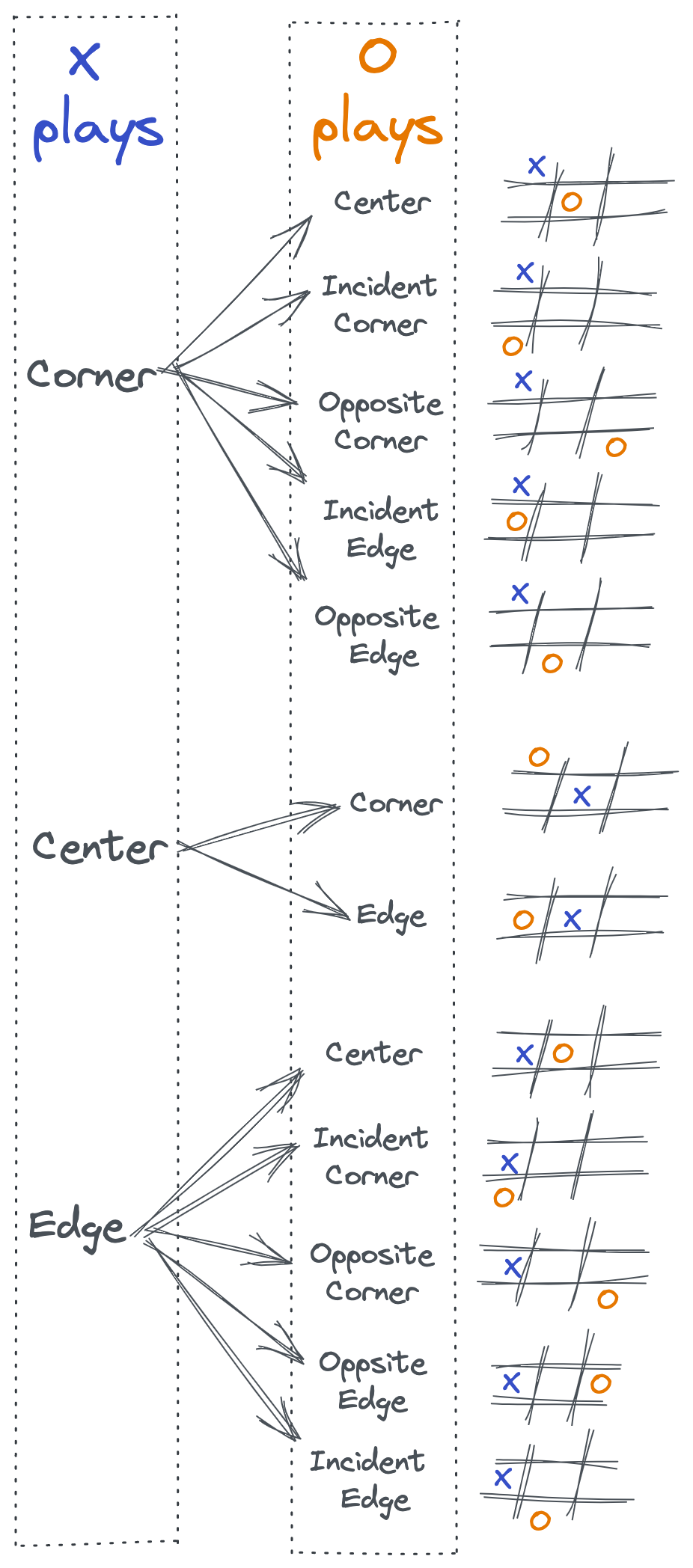
In 7 of them, (X) always wins by applying the following sequence of moves.
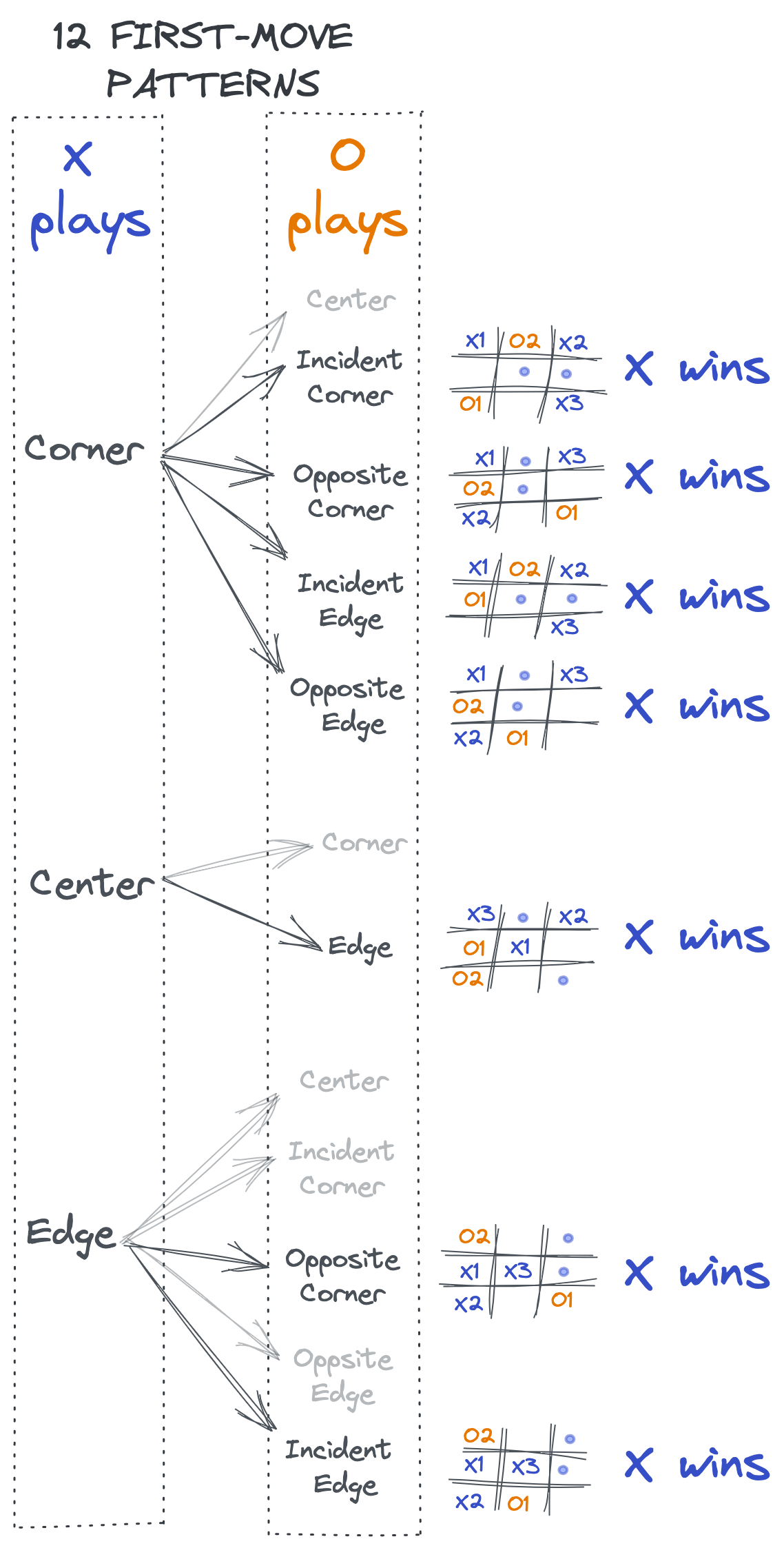
The second player (O) cannot prevent the defeat because her second-move is enforced (she should “block”) and her third-move is irrelevant because (X) has a “fork”.
In the rest of 5 first-move patterns, (X) can always lead the game to a tie. How? (X) enforces a position for which (O) cannot have a fork.